A Simple Python eDSL for Piecewise Relations

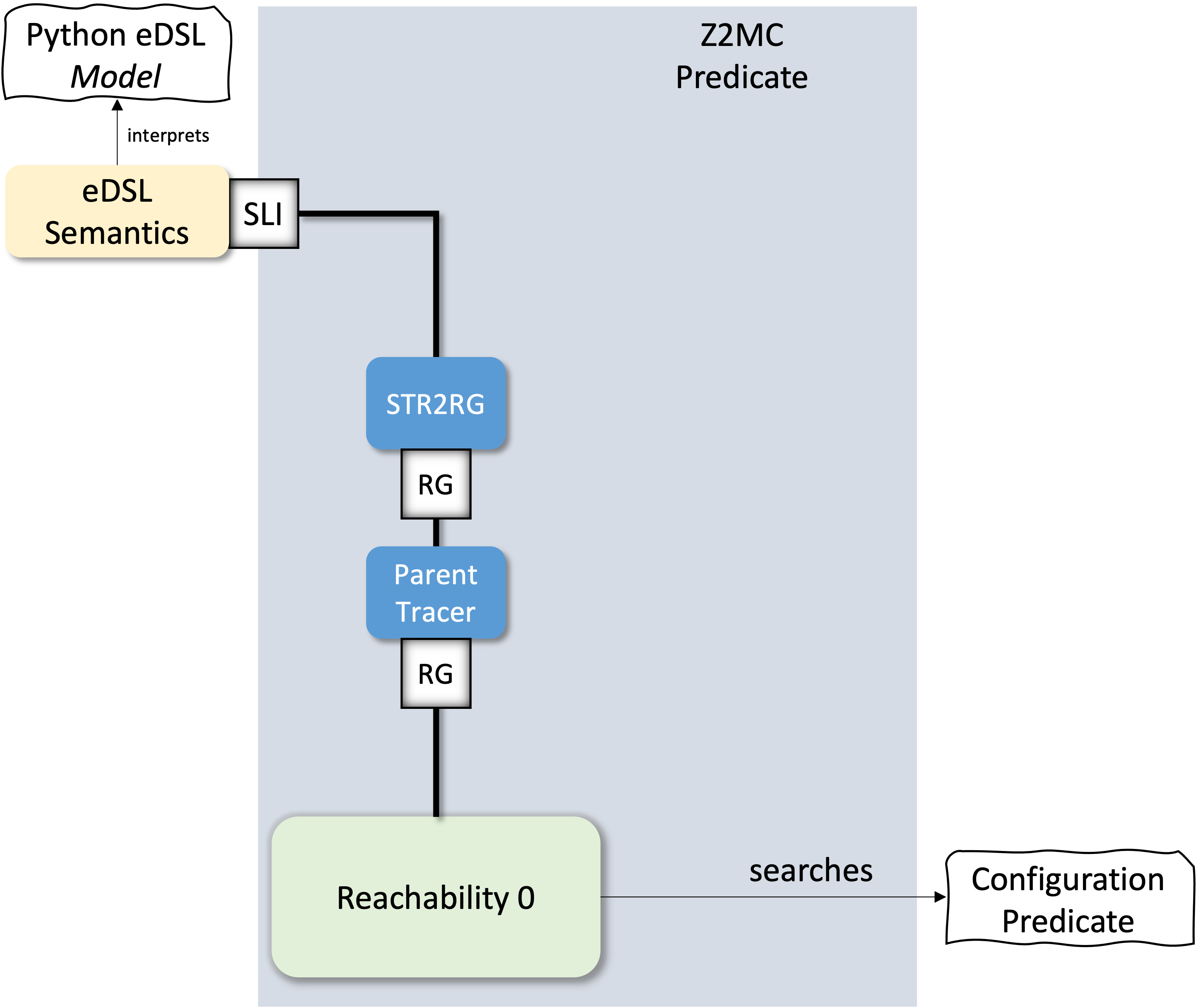{: width="400" style="display:block; margin-left:auto; margin-right:auto"}

Implementing the STR directly works, but looking at our last specifications using the made-up language we see that there is a certain syntactical pollution. To address this issue in this chapter we will create a simple embedded Domain-Specific Language (eDSL) in Python.

Note: Creating an external DSL for our specification language is outside the scope of this work. The interested reader is nevertheless encouraged to try. Such a reader is encouraged to study the TLA+ syntax to find other (rather inspired) operators, which can further simplify the syntax. Readers keen on the graphical syntax could study UML statecharts in conjunction with the AnimUML specification and verification environment to get another more graphical perspective.

Our eDSL will be named Soup, because it will encode the specifications as a soup of pieces necessary to encode the piecewise relations.

The first ingredient, which will encode the valuation of the variables used in a specification is identical to the Configuration concept that we have used for generalizing the Vertex types in the graph abstraction.

For the one-bit clock example we will have:

class OneBitClockConfig:
    def __init__(self, value):
        self.clock = value

    def __hash__(self):
        return hash(self.clock)

    def __eq__(self, other):
        if not isinstance(other, OneBitClockConfig):
            return False
        return self.clock == other.clock

    def __repr__(self):
        return f'clock={self.clock}'

The initialization part of the specification can be decomposed around the disjunctions. Each term in the disjunction will become a unique configuration. Moreover, each such term is required to initialize all the variables. Thus the initialization of the one-bit clock will be defined as follows:

init = [OneBitClockConfig(0), OneBitClockConfig(1)]

Each piece of the relation will be encoded as two lambdas encapsulated in a LambdaPiece object, defined as follows:

class LambdaPiece:
    def __init__(self, name='', guard, generator):
        self.name = name
        self.guard = guard
        self.generator = generator

    def __eq__(self, other):
        if not isinstance(other, LambdaPiece):
            return False
        return self.name == other.name and self.guard == other.guard and self.generator == other.generator

For the one-bit clock specification, we get:

toOne  = LambdaPiece('toOne',  lambda c: OneBitClockConfig(1), lambda c: c.clock == 0)
toZero = LambdaPiece('toZero', lambda c: OneBitClockConfig(0), lambda c: c.clock == 1 )

The specification is captured in a Soup instance, defined as follows:

class Soup:
    def __init__(self, initial=[], pieces=[]):
        self.initial = initial
        self.pieces = pieces

    def add(self, name, guard, generator):
        self.extend(LambdaPiece(name, guard, generator))

    def extend(self, beh):
        if isinstance(beh, LambdaPiece):
            self.pieces.append(beh)
        else:
            self.pieces.extend(beh)

For the one-bit clock specification, the soup is:

one_bit_clock_spec = Soup(init, [toOne, toZero])

To interpret the soup as a piecewise relation, the next step is to implement the semantics as follows:

class RootedPiecewiseRelationSemantics(SemanticTransitionRelation):
    def __init__(self, soup):
        self.soup = soup

    def roots(self):
        return self.soup.initial

    def enabled(self, configuration):
        return list(filter(lambda ga: ga.guard(configuration), self.soup.pieces))

    def execute(self, action, configuration):
        target = copy.deepcopy(configuration)
        the_output = action.generator(target)
        return the_output

Note that in the implementation of the execute function we perform a deepcopy. Is this necessary? Knowing that the generator lambda produces a new configuration each time. Explain and give an example where this is necessary.

By the way, the one-bit specification can be even shorter:

one_bit_clock_spec = Soup(
    [0, 1],
    [
        LambdaPiece('toOne',  lambda c: 1, lambda c: c == 0),
        LambdaPiece('toZero', lambda c: 0, lambda c: c == 1)
    ]
)

Why does it work? Can you explain why we do not strictly need a Configuration object in this case?

It can be rather similar to the spec in the previous chapter if written as follows:

init = [0, 1]
tick = [
        LambdaPiece(lambda c: 1, lambda c: c == 0),
        LambdaPiece(lambda c: 0, lambda c: c == 1)]
spec = Soup(init, tick)

Exercises

Exercise 1: Encode the specifications from the previous chapter using the Soup language. Exercise 2: Create a predicate verification tool for the Soup language.

Exercise 3: Verify the mutual exclusion property on the Soup-based Simple Alice-Bob specification.

Exercise 4: Verify the mutual exclusion property on the Soup-based Flag Alice-Bob specification.

Exercise 5: Verify that Simple Alice-Bob and Flag Alice-Bob are deadlock-free.

Make sure that the results match the ones obtained in the previous chapter. If they don't match find and fix the bugs.

Exercise 6: Encode the Hanoi problem using the Soup language and use the Soup predicate verifier to find the solution.

Exercise 7: TODO: German traffic light and history management.