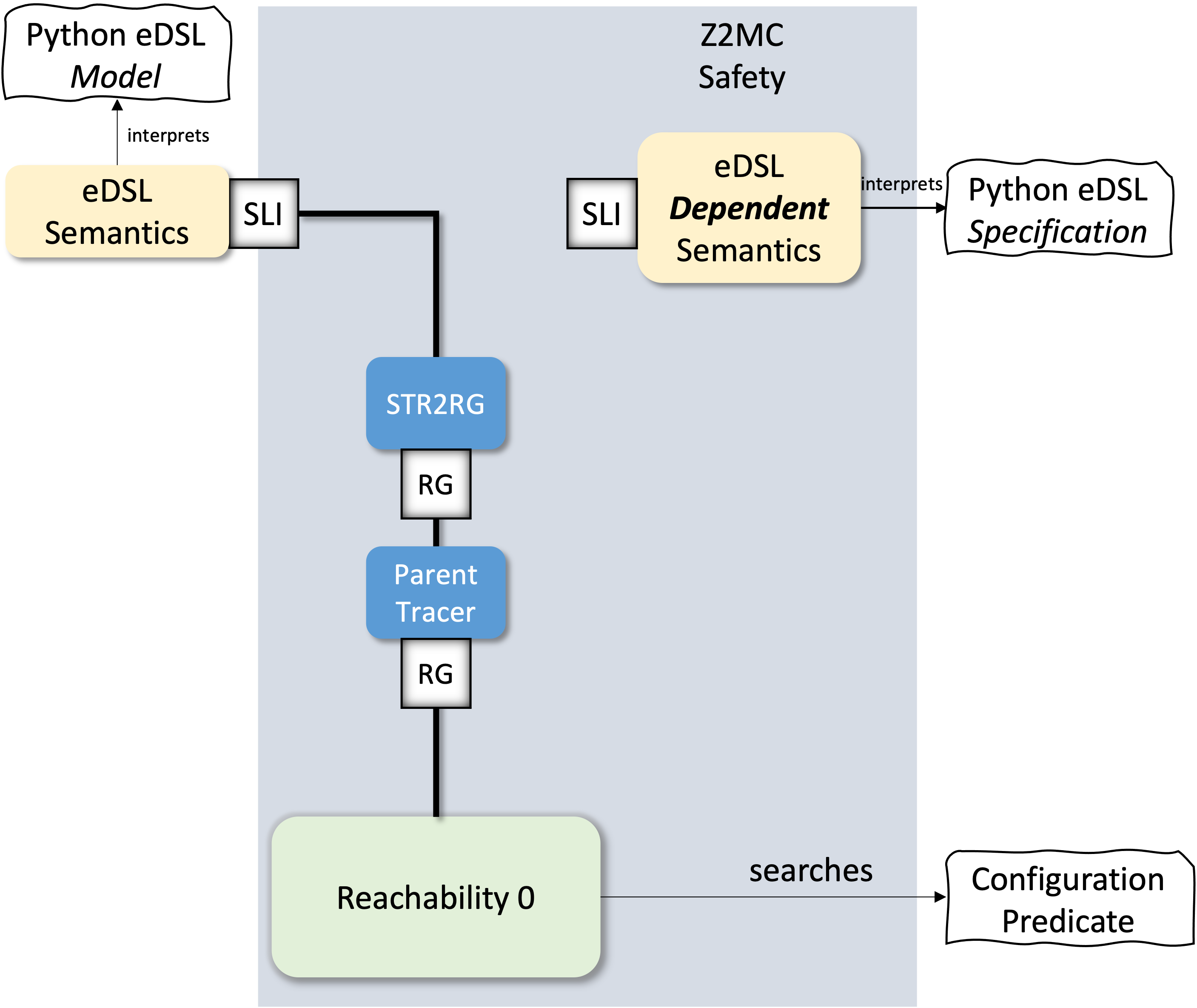
More Expressive Properties Through Dependent Semantics

{: width="400" style="display:block; margin-left:auto; margin-right:auto"}

Until now our verification tasks were limited to predicate verification. To go further we need to extend the expressivity of the "property" language, which was restricted to simple state predicates. To achieve this we will first extend our semantical framework to allow the creation of dependencies between different semantics. The discussion in this chapter is based on the Soup language, which is extended to allow the design of dependent specifications.

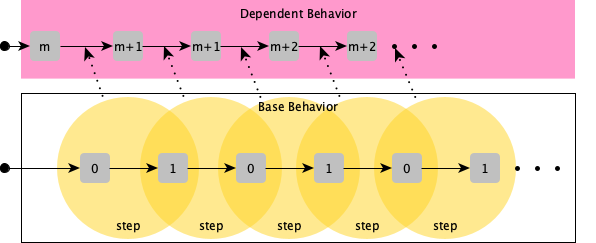
One case where dependent semantics can came in handy is specifying the behaviour of a minute clock based on the ticks of the one-bit clock. The minute variable should be incremented on the rising edge of the one-bit clock.

var minutes
init ≜ minutes ∈ {1..60}             -- note the non-deterministic assignement
tick ≜ minutes' = (minutes + 1) % 60 + 1 if clock = 0 ∧ clock' = 1
spec ≜ init ∧ ☐(tick ∨ minutes' = minutes)

{: style="display:block; margin-left:auto; margin-right:auto"}

Another example is the hour clock based on the minute clock.

var hour
init ≜ hour ∈ {1..12}             -- note the non-deterministic assignement
tick ≜ hour' = (hour + 1) % 12 + 1 if minutes = 60
spec ≜ init ∧ ☐(tick ∨ hour' = hour)

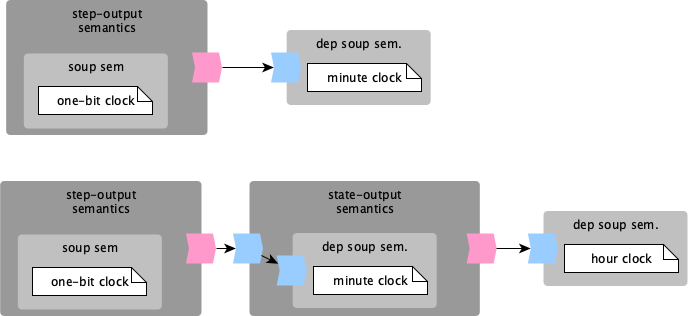
If we are looking at these previous specification they seem incomplete. The minute clock specification defines its behaviour relatively to another behavior, from which it can extract a notion of clock. The name clock is used in the minute-clock but its behaviour is never defined.

{: style="display:block; margin-left:auto; margin-right:auto"}

We define a dependent semantics as a semantics that requires some additional input (of type I), besides the current configuration (of type C), to:

1. decide what is the set of enabled actions. If The actions function signature becomes actions: I → C → set A.
2. compute the target configuration set, during the execution of an action. The execute signature becomes execute: A → I → C → set C.

Now that we have an input-dependent semantics, we can define an output producing semantics to improve the symmetry of our design. Such a semantics should produce an output during the execution of a step, in such a way that is possible to connect it to the an input-dependent semantics. To achieve this, we extend the signature of the execute function: execute: A → I → C → set (O × C). During the execution of an action an output O is produced, besides the new configuration.

With these two ideas our semantically framework evolves, to something very similar to Mealy abstract machines. The execution step is dependent on the current configuration, and the input. Action execution effectivelly computes the next comfiguration and the output. Thus a step in the semantics state-space becomes:

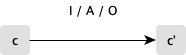{: style="display:block; margin-left:auto; margin-right:auto"}

class RootedPiecewiseRelationDependentSemantics:

    def __init__(self, soup):
        self.soup = soup

    def roots(self):
        return self.soup.initial

    def enabled(self, input, configuration):
        return list(filter(lambda ga: ga.guard(input, configuration), self.soup.pieces))

    def execute(self, action, input, configuration):
        target = copy.deepcopy(configuration)
        the_output = action.generator(input, target)
        return the_output

class ToStepOutputSemantics:

    def __init__(self, subject):
        self.subject = subject

    def roots(self):
        return self.subject.initial

    def enabled(self, configuration):
        return self.subject.enabled

    def execute(self, action, configuration):
        the_targets = self.subject.execute(action, configuration)
        
        return list(map(lambda t: ((configuration, action, t), t), the_targets))